@grifferz@social.bitfolk.com2026-01-23 03:30:20
I'm having a right bugger of a time upgrading my desktop from Debian 12 to 13 (trixie). Of course it's down to NVIDIA.
It has a GTX 1080 Ti which worked mostly okay under Debian 12 and version 535.something of their drivers. I was a little disappointed to find I still had to hack udev rules to convince gdm to offer a Wayland session. Finally get into Wayland and find it spams me with kernel OOPS:
@metacurity@infosec.exchange2025-11-11 14:50:16
Check out today's Metacurity for a comprehensive run-down of crucial cybersecurity developments you should know, including
--Yanluowang initial access broker faces up to 53 years in prison following guilty plea,
--CBO breach is considered 'ongoing,'
--Asahi's shipments are at 10% following attack and ahead of holiday season,
--Payments by British insurers for cyber incidents have tripled,
--Chinese national faces UK sentencing this week for money …
@arXiv_mathOC_bot@mastoxiv.page2025-11-14 09:41:00
Minimizing smooth Kurdyka-{\L}ojasiewicz functions via generalized descent methods: Convergence rate and complexity
Masoud Ahookhosh, Susan Ghaderi, Alireza Kabgani, Morteza Rahimi
https://arxiv.org/abs/2511.10414 https://arxiv.org/pdf/2511.10414 https://arxiv.org/html/2511.10414
arXiv:2511.10414v1 Announce Type: new
Abstract: This paper addresses the generalized descent algorithm (DEAL) for minimizing smooth functions, which is analyzed under the Kurdyka-{\L}ojasiewicz (KL) inequality. In particular, the suggested algorithm guarantees a sufficient decrease by adapting to the cost function's geometry. We leverage the KL property to establish the global convergence, convergence rates, and complexity. A particular focus is placed on the linear convergence of generalized descent methods. We show that the constant step-size and Armijo line search strategies along a generalized descent direction satisfy our generalized descent condition. Additionally, for nonsmooth functions by leveraging the smoothing techniques such as forward-backward and high-order Moreau envelopes, we show that the boosted proximal gradient method (BPGA) and the boosted high-order proximal-point (BPPA) methods are also specific cases of DEAL, respectively. It is notable that if the order of the high-order proximal term is chosen in a certain way (depending on the KL exponent), then the sequence generated by BPPA converges linearly for an arbitrary KL exponent. Our preliminary numerical experiments on inverse problems and LASSO demonstrate the efficiency of the proposed methods, validating our theoretical findings.
toXiv_bot_toot
@usul@piaille.fr2025-12-04 05:09:37
Delyan Peevski, le puissant oligarque qui met les Bulgares dans la rue
https://www.lemonde.fr/international/article/2025/12/04/delyan-peevski-le-puissant-oligarque-qui-met-les-bulgares-dans-la-rue_…
@arXiv_mathOC_bot@mastoxiv.page2025-11-14 09:50:00
(Adaptive) Scaled gradient methods beyond locally Holder smoothness: Lyapunov analysis, convergence rate and complexity
Susan Ghaderi, Morteza Rahimi, Yves Moreau, Masoud Ahookhosh
https://arxiv.org/abs/2511.10425 https://arxiv.org/pdf/2511.10425 https://arxiv.org/html/2511.10425
arXiv:2511.10425v1 Announce Type: new
Abstract: This paper addresses the unconstrained minimization of smooth convex functions whose gradients are locally Holder continuous. Building on these results, we analyze the Scaled Gradient Algorithm (SGA) under local smoothness assumptions, proving its global convergence and iteration complexity. Furthermore, under local strong convexity and the Kurdyka-Lojasiewicz (KL) inequality, we establish linear convergence rates and provide explicit complexity bounds. In particular, we show that when the gradient is locally Lipschitz continuous, SGA attains linear convergence for any KL exponent. We then introduce and analyze an adaptive variant of SGA (AdaSGA), which automatically adjusts the scaling and step-size parameters. For this method, we show global convergence, and derive local linear rates under strong convexity.
toXiv_bot_toot
@usul@piaille.fr2025-10-28 03:37:00
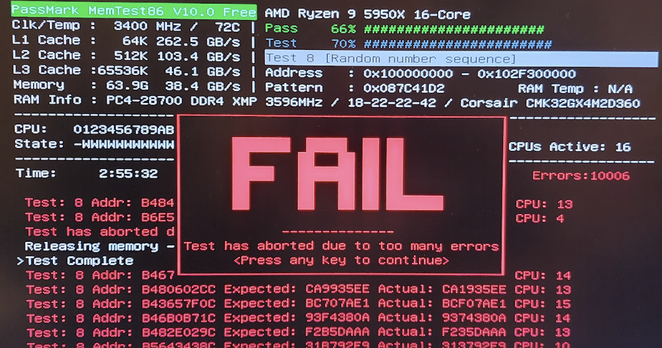
Hardware is weird sometimes
Julien's random thoughts: Corsair CMK32GX4M2D3600 RAM Micron single-rank kit vs CMK32GX4M2D3600 Nunya dual-rank RAM kit vs Asus Prime X570 Pro motherboard
https://blog.madbrain.com/2022/12/corsair-cmk32gx4m2d3600-ram-micron.…
