Tootfinder

49ers' Brock Purdy has never lost in Seattle: Seahawks facing their worst nightmare in NFL playoffs

https://www.cbssports.com/nfl/news/49ers-brock-purdy-has-never-lost-i…

Totally paracompact spaces and the Menger covering property
Davide Giacopello, Maddalena Bonanzinga, Piotr Szewczak
https://arxiv.org/abs/2511.10252 https://arxiv.org/pdf/2511.10252 https://arxiv.org/html/2511.10252
arXiv:2511.10252v1 Announce Type: new
Abstract: A topological space is totally paracompact if any base of this space contains a locally finite subcover. We focus on a problem of Curtis whether in the class of regular Lindel\"of spaces total paracompactness is equivalent to the Menger covering property. To this end we consider topological spaces with certain dense subsets. It follows from our results that the above equivalence holds in the class of Lindel\"of GO-spaces defined on subsets of reals. We also provide a game-theoretical proof that any regular Menger space is totally paracompact and show that in the class of first-countable spaces the Menger game and a partial open neighborhood assignment game of Aurichi are equivalent. We also show that if $\mathfrak{b}=\omega_1$, then there is an uncountable subspace of the Sorgenfrey line whose all finite powers are Lindel\"of, which is a strengthening of a famous result due to Michael.
toXiv_bot_toot

🇺🇦 Auf radioeins läuft...
Buffy Sainte-Marie:
🎵 The Circle Game
#NowPlaying #BuffySainteMarie
https://kisszanto.bandcamp.com/track/buffy-sainte-marie-the-circle-game-kisszanto-ethno-folk-rave-mix
https://open.spotify.com/track/5TTBGJd8Fkr66OX8j8adCH

I'm listening to the music track of the yet to be released Netflix "Train Dreams" by Dessner. (He also did the interesting music for the "Manhunt" series.)
It seems to me that some of the better compositions and performances are in sound tracks and credits of movies and series.
(Such as the "Strange Game" tune by Mick Jagger in the Slow Horses series. But perhaps the greatest are some older things, like the B. Hermann music from Hitchock's …

Betaal jij meer of minder belasting dan Elon Musk?
https://maps.greenpeace.org/gpafrica/billionaire-taxometer/

The Billionaire Taxometer
Can you beat Musk at his own game?

Jason Proctor is contributing to the CBC's live blog scroll from a legal perspective and as always, his stuff is illumniating. I'll paste his report in because it can get lost in the scroll easily.
"Creditors circle as cull looms
Jason Proctor
I'm Jason Proctor, a reporter with CBC Vancouver who looked into a series of lawsuits facing the owners of Universal Ostrich Farms Inc.
Last month, I spoke with three creditors who are watching today's ruling with great interest — and some skin in the game.
B.C. Supreme Court judges have ordered the farm's owners to repay debts worth more than $250,000 but, up until now, the creditors have been unable to collect. Normally in this kind of situation, a creditor would move to seize the business assets — but because in this case those assets are ostriches caught up in a legal battle, that's been challenging, to say the least.
All three creditors have tried to garnish the CFIA to intercept any money the agency might pay out as compensation for killing the birds (potentially up to $3,000 a bird, the CFIA says) but it remains to be seen how that will work. The creditors, however, told me they are anxious to recoup their losses.”
https://www.cbc.ca/news/canada/british-columbia/livestory/bc-ostrich-farm-decision-scoc-9.6968394?ts=1762453717737

When you beat the later levels, Linux restarts the whole game over but in hard mode. Sure, I've installed MySQL on Debian before, but this time around there's extra challenges - like the GPG signature on <https://dev.mysql.com/doc/refman/8.4/en/checking-gpg-signature…

WATCH! EU launches €90B for Ukraine | War hits Russia | Trump’s sanctions game: https://benborges.xyz/2025/12/20/watch-eu-launches-b-for.html

Certain results on selection principles associated with bornological structure in topological spaces
Debraj Chandra, Subhankar Das, Nur Alam
https://arxiv.org/abs/2511.04038 https://arxiv.org/pdf/2511.04038 https://arxiv.org/html/2511.04038
arXiv:2511.04038v1 Announce Type: new
Abstract: We study selection principles related to bornological covers in a topological space $X$ following the work of Aurichi et al., 2019, where selection principles have been investigated in the function space $C_\mathfrak{B}(X)$ endowed with the topology $\tau_\mathfrak{B}$ of uniform convergence on bornology $\mathfrak{B}$. We show equivalences among certain selection principles and present some game theoretic observations involving bornological covers. We investigate selection principles on the product space $X^n$ equipped with the product bornolgy $\mathfrak{B}^n$, $n\in \omega$. Considering the cardinal invariants such as the unbounding number ($\mathfrak{b}$), dominating numbers ($\mathfrak{d}$), pseudointersection numbers ($\mathfrak{p}$) etc., we establish connections between the cardinality of base of a bornology with certain selection principles. Finally, we investigate some variations of the tightness properties of $C_\mathfrak{B}(X)$ and present their characterizations in terms of selective bornological covering properties of $X$.
toXiv_bot_toot

Broncos vs. Cowboys radio coverage: Station, channel, streaming to listen live to NFL Week 8 game broadcast https://www.sportingnews.com/us/nfl/news/broncos-cowboys-radio-coverage-station-channels-streaming-lis…

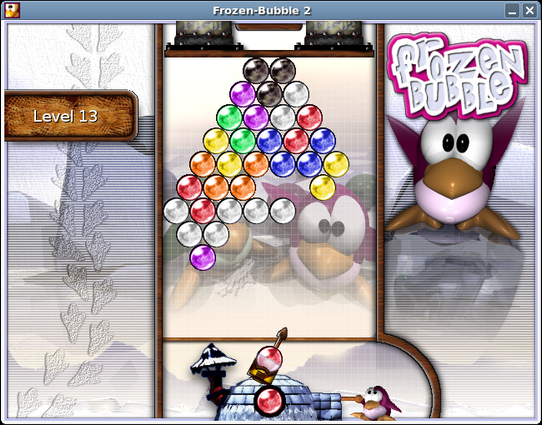
You all deserve a break; so for my last #freesoftwareadvent I suggest the game
'Frozen bubble':
https://en.wikipedia.org/wiki/Frozen_Bubble

Frozen Bubble - Wikipedia

One of my favorite mastodon features is the time-based muting. Someone's posting through (suffering, lol) a football game, and I have less than zero interest in sportsball? But I generally enjoy following them? Mute them for 1 hour (or 6 hours), and my screen is no longer littered with crap about touchzonegoalruns.
Or maybe you don't want to see my stupid replies to a dumb horror movie from 40 years ago? Mute me for an hour or two, and voila!

Omg, patently wrong. To begin with, I am the one using the GTX 1650, and my video shows that it's working great even with DLSS, as opposed to the viewer with the AMD problem. And that parrotting nincompoop of an AI wants me to - what? - save time, give technical advice, make some small talk? What a big, smoking hot, pointless pile of b this technology turns out to be.
And I guess Google lets the same fucking stupid LM to determine how to recommend my video to other viewers? Great!<…

Raiders Final Injury Report Before Week 7 Game https://www.si.com/nfl/raiders/las-vegas-brock-bowers-kansas-city-chiefs-maxx-crosby-jakobi-meyers

What channel is Broncos vs. Cowboys on today? Live stream, time, TV schedule to watch NFL Week 8 game https://www.sportingnews.com/us/nfl/news/broncos-cowboys-channel-stream-time-schedule-watch-nfl/d7f9109894d61bbe238ac7c0

Odell Beckham Jr. reinstated after NFL suspension: Five landing spots for three-time Pro Bowl receiver

https://www.cbssports.com/nfl/news/odell-beckham-jr-free-agent-l…

Hangin' With The 'Boys: Can’t Miss a Beat https://www.dallascowboys.com/podcast/hangin-with-the-boys-can-t-miss-a-beat