Tootfinder

Dilepton angular distributions in the color-dipole $S$-matrix framework
Yan B. Bandeira, Victor P. Goncalves, Wolfgang Sch\"afer
https://arxiv.org/abs/2507.06207

Dilepton angular distributions in the color-dipole $S$-matrix framework
The dilepton production at forward rapidities in hadronic collisions at the LHC energies is considered and the helicity density matrix elements of gauge bosons that enter the Drell--Yan angular coefficients associated with the gauge boson decay ($G = γ^*, Z^0, W$) are derived using the color-dipole $S$ - matrix framework. We show results for $pp$ collisions at $\sqrt{s} = 14$ TeV for the nonvanishing helicity density matrix elements in the rapidity range of $2.0 \le y \le 4.0$ of the gauge bos…

FACT: the Features At Convergence Theorem for neural networks
Enric Boix-Adsera, Neil Mallinar, James B. Simon, Mikhail Belkin
https://arxiv.org/abs/2507.05644

FACT: the Features At Convergence Theorem for neural networks
A central challenge in deep learning theory is to understand how neural networks learn and represent features. To this end, we prove the Features at Convergence Theorem (FACT), which gives a self-consistency equation that neural network weights satisfy at convergence when trained with nonzero weight decay. For each weight matrix $W$, this equation relates the "feature matrix" $W^\top W$ to the set of input vectors passed into the matrix during forward propagation and the loss gradients passed t…

Heute auf'm Weg zur Arbeit: einige Silberreiher und Löffler, viele Graureiher, Schwanen- und Entenfamilien.
Und angenehm warmer Rückenwind!
#mdrza

5 #Grafana in #Docker examples to get started with metrics, logs, and traces
https://

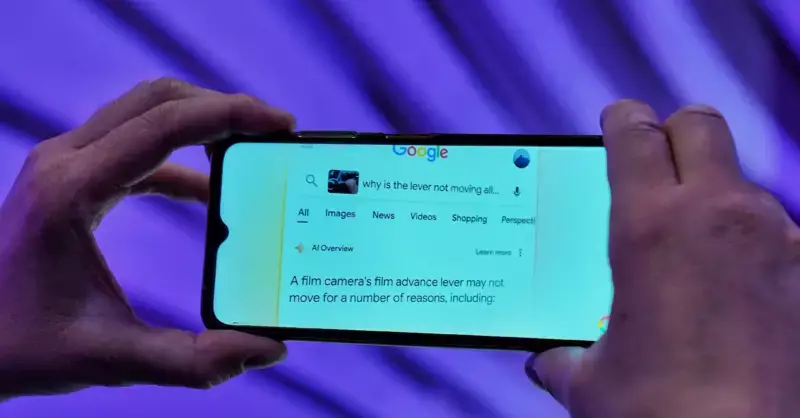
Analysis: Mail Online is among major news brands most-impacted by Google's AI Overviews, with 68.8% of the top 100 keyword searches resulting in no site visits (Charlotte Tobitt/Press Gazette)
https://press…

How Google AI Overviews is fuelling zero-click searches for top publishers
New Similarweb data shows likes of Mail Online and People see high proportion of AI Overviews for their key search terms.

Fixed Point Theorems for Kannan and Chatterjea-type Mappings in Probabilistic Cone Metric Spaces
Elvin Rada
https://arxiv.org/abs/2509.06962 https://arxiv.…

Fixed Point Theorems for Kannan and Chatterjea-type Mappings in Probabilistic Cone Metric Spaces
This paper establishes novel fixed point theorems for Kannan-type and Chatterjea-type mappings in probabilistic cone metric spaces. By integrating probabilistic distance functions with cone-valued structures, we generalize classical fixed point results to settings with inherent uncertainty. Our approach leverages the distributional properties of probabilistic metrics and the order structure of cones to develop contraction conditions ensuring the existence and uniqueness of fixed points. Applica…

Langtauferer
Today, a year ago, I ventured on a dream trip I'd been researching for a long time, and which ended up being a semi-religious experience, being immersed in (and somewhat overwhelmed by) an actively changing environment, the upheaval and plethora of geological features, structures, unreal colors, layers, textures and the "wounds" exposed by the melting and disappearing glaciers... Countless waterfalls, stunning erosion features, later traversing the glacier ga…

This https://arxiv.org/abs/2505.23440 has been replaced.
initial toot: https://mastoxiv.page/@arXiv_mat…

Comparison of total $σ_k$-curvature
Volume comparison theorem is a type of fundamental results in Riemannian geometry. In this article, we extend the volume comparison result in \cite{Besse2008} to the comparison of total $σ_l$-curvature with respect to $σ_k$-curvature ($l

On the Gromov--Hausdorff stability of metric viscosity solutions
Shimpei Makida
https://arxiv.org/abs/2507.06495 https://arxiv.org/pdf/2507.06495 https://arxiv.org/html/2507.06495
arXiv:2507.06495v1 Announce Type: new
Abstract: We establish the stability of metric viscosity solutions to first-order Hamilton--Jacobi equations under Gromov--Hausdorff convergence. Our proof combines a characterization of metric viscosity solutions via quadratic distance functions with a doubling variable method adapted to epsilon-isometries, which allows us to pass to the Gromov--Hausdorff limit without embedding the spaces into a common ambient space. As a byproduct, we give a PDE-based proof of the stability of the dual Kantorovich problems under measured-Gromov--Hausdorff convergence.
toXiv_bot_toot

Inequalities for Standard Model Yukawa Couplings
Gero von Gersdorff, Lucas Modesto
https://arxiv.org/abs/2506.06423 https://arxiv.org…

Inequalities for Standard Model Yukawa Couplings
We show that the Standard Model Yukawa matrices satisfy a set of simple yet nontrivial inequalities. The relations we derive are independent of the basis used to define the fermion fields, and, amongst other things, place strong constraints on the alignment of the columns of the up-type and down-type Yukawa matrices, as well as their cofactor matrices. The reason why one can obtain such strong statements can be traced back to the hierarchical nature of the fermion masses and quark mixings. The …