@servelan@newsie.social2026-01-22 06:38:27
Republicans Are Preparing for Forced Birth Coachella
https://jessica.substack.com/p/march-for-life-roe-anniversary?open=false#§local-idaho-officials-say-womens-health-is-too-niche-to-fund
@frankel@mastodon.top2025-12-21 11:00:05
@netzschleuder@social.skewed.de2025-12-21 10:00:03
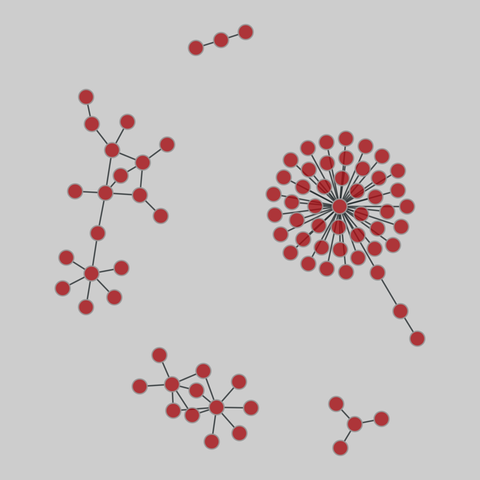
baseball: Baseball steroid use (2008)
Two networks representing steroid use among baseball players. First, a bipartite network of players and their steroid providers (of illegal performance-enhancing substances). Second, a one-mode projection of players, which are linked if they have a common supplier.
This network has 84 nodes and 84 edges.
Tags: Social, Offline, Weighted, Projection
@Techmeme@techhub.social2025-12-18 09:25:57
An in-depth look at a recent research paper that offered a roadmap to the viability of 3D HBM-on-GPU integration for improved AI performance and utilization (More Than Moore)
https://morethanmoore.substack.com/p/solving-the-problems-of-hbm-on-logic
<…
@mlawton@mstdn.social2025-12-20 18:07:13
VAR does its job, but I think its very presence allows the referee to underwhelm on the initial decision. He’s got cover, so why extend? It’s not supposed to be used in that manner, but I can understand why they do.
The natural question is if they are “clear and obvious errors”, how does an overturn affect PGMOL’s evaluation of a referees performance? I think it doesn’t, because PFMOL is corrupt and has no desire to improve. Just gaslight, baby. Gaslight.
@Techmeme@techhub.social2026-01-19 10:45:37
Chinese smartphone shipments fell 1.6% YoY in Q4 2025 and 0.6% YoY for 2025 due to weak demand, rising prices, and memory shortages; iPhone shipments rose 28% (Counterpoint Research)
https://counterpointresearch.com/en/insights/China-Smartphone-Shipments-Q4-20…
@inthehands@hachyderm.io2025-12-18 16:47:12
We desperately need to figure out how to flip this: how to lift up the creators of wonderful things, instead of rewarding whoever can acquire power over their creations.
I don’t think we know how to do this. There’s a vast spectrum of schemes for fixing this, ranging from capitalist versions of “intellectual property” to Marxist “just end capitalism” notions to various versions of “easy, society should just be different.” I find them all lacking, both in theory and in practice. This is a problem that’s existed for millennia, not decades, and I’m not convinced we have a clear solution.
4/
@cdarwin@c.im2026-01-18 05:45:49
As Donald Trump ramped up his threats against the people he is supposed to be working for,
his administration’s extreme immigration enforcement led Homeland Security Secretary Kristi Noem to admit that anyone
— U.S. citizen or otherwise
— should be prepared to have to prove their citizenship to DHS agents.
Asked Thursday about U.S. citizens being asked to provide proof of citizenship in Minnesota
and whether that is “targeted enforcement,”
Noem said the f…
@netzschleuder@social.skewed.de2026-01-17 22:00:04
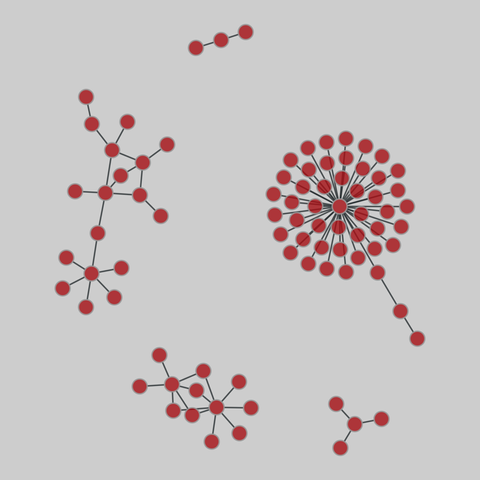
baseball: Baseball steroid use (2008)
Two networks representing steroid use among baseball players. First, a bipartite network of players and their steroid providers (of illegal performance-enhancing substances). Second, a one-mode projection of players, which are linked if they have a common supplier.
This network has 84 nodes and 84 edges.
Tags: Social, Offline, Weighted, Projection
@netzschleuder@social.skewed.de2026-02-17 05:00:03
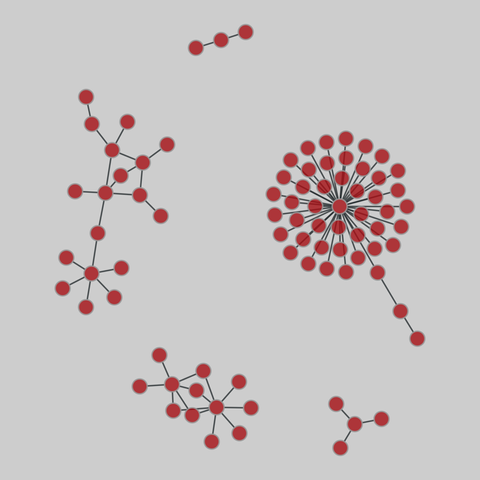
baseball: Baseball steroid use (2008)
Two networks representing steroid use among baseball players. First, a bipartite network of players and their steroid providers (of illegal performance-enhancing substances). Second, a one-mode projection of players, which are linked if they have a common supplier.
This network has 84 nodes and 84 edges.
Tags: Social, Offline, Weighted, Projection
