@seeingwithsound@mas.to2025-12-10 10:36:04
Can a visual neuroprosthesis communicate with the brain? https://www.medscape.com/viewarticle/can-visual-neuroprosthesis-communicate-brain-2025a1000yhe Archived at
@UP8@mastodon.social2025-11-11 22:47:33
🫰🏿 Snap out of it: Canonical on Flatpak friction, Core Desktop, and the future of Ubuntu
https://go.theregister.com/feed/www.theregister.com/2025/11/03/canonical_jon_seager_qa/
@midtsveen@social.linux.pizza2025-12-11 21:07:06
Ah yes, the three comrades, affectionate today, ideological enemies tomorrow!
#Anarchism #Syndicalism #AnarchoSyndicalism
@blakes7bot@mas.torpidity.net2025-11-10 07:04:42
#Blakes7 Series B, Episode 13 - Star One
AVON: [On communicator] What is it, Jenna?
JENNA: There's a ship, its coming in for a surface landing.
AVON: [On communicator] Have they spotted you?
JENNA: I've got the detector shield up.
@EarthOrgUK@mastodon.energy2025-11-10 03:23:04
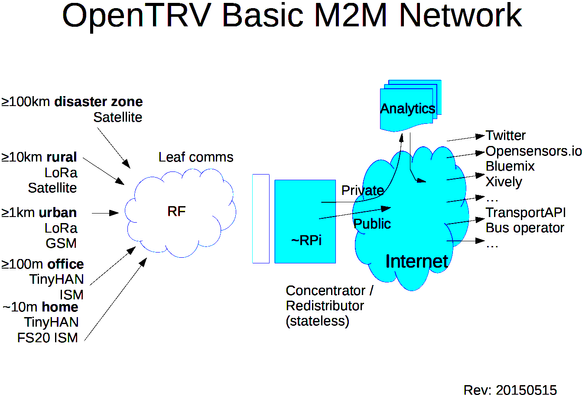
On IoT Communications Backhaul (2015) - How small Internet-of-Things (IoT) devices should talk to one another. #IoT #comms - https://www.
@brichapman@mastodon.social2026-01-11 16:31:00
Brooklyn's getting a massive EV charging upgrade.
A new Williamsburg hub is launching with 88 fast charging ports—each delivering up to 300 kW. The game-changer? Battery storage that captures off-peak electricity and deploys it during rush hours, making charging cheaper and greener.
https://
@vosje62@mastodon.nl2026-01-09 05:27:32
@arXiv_csGT_bot@mastoxiv.page2025-12-09 07:47:37
The Communication Complexity of Combinatorial Auctions with Additional Succinct Bidders
Frederick V. Qiu, S. Matthew Weinberg, Qianfan Zhang
https://arxiv.org/abs/2512.06585 https://arxiv.org/pdf/2512.06585 https://arxiv.org/html/2512.06585
arXiv:2512.06585v1 Announce Type: new
Abstract: We study the communication complexity of welfare maximization in combinatorial auctions with bidders from either a standard valuation class (which require exponential communication to explicitly state, such as subadditive or XOS), or arbitrary succinct valuations (which can be fully described in polynomial communication, such as single-minded). Although succinct valuations can be efficiently communicated, we show that additional succinct bidders have a nontrivial impact on communication complexity of classical combinatorial auctions. Specifically, let $n$ be the number of subadditive/XOS bidders. We show that for SA $\cup$ SC (the union of subadditive and succinct valuations): (1) There is a polynomial communication $3$-approximation algorithm; (2) As $n \to \infty$, there is a matching $3$-hardness of approximation, which (a) is larger than the optimal approximation ratio of $2$ for SA, and (b) holds even for SA $\cup$ SM (the union of subadditive and single-minded valuations); and (3) For all $n \geq 3$, there is a constant separation between the optimal approximation ratios for SA $\cup$ SM and SA (and therefore between SA $\cup$ SC and SA as well). Similarly, we show that for XOS $\cup$ SC: (1) There is a polynomial communication $2$-approximation algorithm; (2) As $n \to \infty$, there is a matching $2$-hardness of approximation, which (a) is larger than the optimal approximation ratio of $e/(e-1)$ for XOS, and (b) holds even for XOS $\cup$ SM; and (3) For all $n \geq 2$, there is a constant separation between the optimal approximation ratios for XOS $\cup$ SM and XOS (and therefore between XOS $\cup$ SC and XOS as well).
toXiv_bot_toot
@midtsveen@social.linux.pizza2026-01-10 17:22:19
Blue Meanie Mushrooms 🍄 DoubleBlind
#Psychedelic #BlueMeanie
@blakes7bot@mas.torpidity.net2025-11-11 19:11:51
Series A, Episode 05 - The Web
GEELA: Come with us, please.
[Blake follows Geela and Novara back through the room and into the lounge area. His communicator chimes.]
BLAKE: [Into communicator.] Blake.
AVON: [V.O.] Avon.
BLAKE: You ready?
https://blake.torpidity.net/m/105/415
