@seeingwithsound@mas.to2025-12-10 10:36:04
Can a visual neuroprosthesis communicate with the brain? https://www.medscape.com/viewarticle/can-visual-neuroprosthesis-communicate-brain-2025a1000yhe Archived at
@servelan@newsie.social2025-10-11 16:47:59
National Coming Out Day: For LGBTQ refugees, coming out isn't a choice
https://www.thepinknews.com/2025/10/11/lgbtq-refugee-asylum-national-coming-out-day/
@blakes7bot@mas.torpidity.net2025-11-10 07:04:42
#Blakes7 Series B, Episode 13 - Star One
AVON: [On communicator] What is it, Jenna?
JENNA: There's a ship, its coming in for a surface landing.
AVON: [On communicator] Have they spotted you?
JENNA: I've got the detector shield up.
@midtsveen@social.linux.pizza2026-01-10 17:22:19
Blue Meanie Mushrooms 🍄 DoubleBlind
#Psychedelic #BlueMeanie
@EarthOrgUK@mastodon.energy2025-11-10 03:23:04
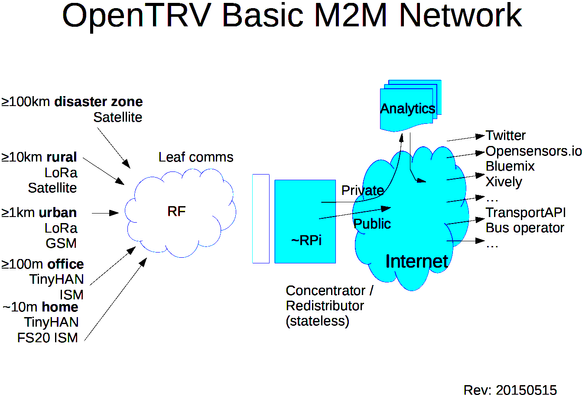
On IoT Communications Backhaul (2015) - How small Internet-of-Things (IoT) devices should talk to one another. #IoT #comms - https://www.
@vosje62@mastodon.nl2026-01-09 05:27:32
@DrPlanktonguy@ecoevo.social2025-10-11 13:45:28
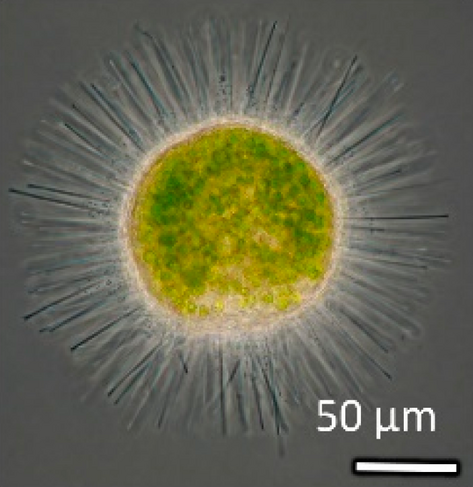
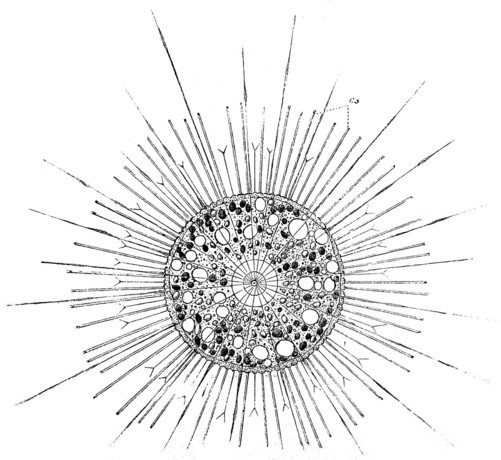
Weekend #Plankton Factoid 🦠🦐
Heliozoans are a group of amoeboid protists found commonly in both fresh and saltwater. They were termed sun-animalcules due to their spherical shape and distinctive radiating microtubules, which support axiopods used to capture food and facilitate movement. Some will also capture symbiotic algal cells which provide energy through photosynthesis. Heliozoa is &quo…
@arXiv_csGT_bot@mastoxiv.page2025-12-09 07:47:37
The Communication Complexity of Combinatorial Auctions with Additional Succinct Bidders
Frederick V. Qiu, S. Matthew Weinberg, Qianfan Zhang
https://arxiv.org/abs/2512.06585 https://arxiv.org/pdf/2512.06585 https://arxiv.org/html/2512.06585
arXiv:2512.06585v1 Announce Type: new
Abstract: We study the communication complexity of welfare maximization in combinatorial auctions with bidders from either a standard valuation class (which require exponential communication to explicitly state, such as subadditive or XOS), or arbitrary succinct valuations (which can be fully described in polynomial communication, such as single-minded). Although succinct valuations can be efficiently communicated, we show that additional succinct bidders have a nontrivial impact on communication complexity of classical combinatorial auctions. Specifically, let $n$ be the number of subadditive/XOS bidders. We show that for SA $\cup$ SC (the union of subadditive and succinct valuations): (1) There is a polynomial communication $3$-approximation algorithm; (2) As $n \to \infty$, there is a matching $3$-hardness of approximation, which (a) is larger than the optimal approximation ratio of $2$ for SA, and (b) holds even for SA $\cup$ SM (the union of subadditive and single-minded valuations); and (3) For all $n \geq 3$, there is a constant separation between the optimal approximation ratios for SA $\cup$ SM and SA (and therefore between SA $\cup$ SC and SA as well). Similarly, we show that for XOS $\cup$ SC: (1) There is a polynomial communication $2$-approximation algorithm; (2) As $n \to \infty$, there is a matching $2$-hardness of approximation, which (a) is larger than the optimal approximation ratio of $e/(e-1)$ for XOS, and (b) holds even for XOS $\cup$ SM; and (3) For all $n \geq 2$, there is a constant separation between the optimal approximation ratios for XOS $\cup$ SM and XOS (and therefore between XOS $\cup$ SC and XOS as well).
toXiv_bot_toot
@Techmeme@techhub.social2025-11-11 11:39:09
Sources: Meta Chief AI Scientist Yann LeCun plans to leave in the coming months to found his own startup; a source says he is in early talks to raise funds (Financial Times)
https://www.ft.com/content/c586eb77-a16e-4363-ab0b-e877898b70de
@blakes7bot@mas.torpidity.net2025-11-11 19:11:51
Series A, Episode 05 - The Web
GEELA: Come with us, please.
[Blake follows Geela and Novara back through the room and into the lounge area. His communicator chimes.]
BLAKE: [Into communicator.] Blake.
AVON: [V.O.] Avon.
BLAKE: You ready?
https://blake.torpidity.net/m/105/415
