Tootfinder

Canonical Ramsey: triangles, rectangles and beyond
Yijia Fang, Gennian Ge, Yang Shu, Qian Xu, Zixiang Xu, Dilong Yang
https://arxiv.org/abs/2510.11638 https://

Canonical Ramsey: triangles, rectangles and beyond
In a seminal work, Cheng and Xu showed that if $S$ is a square or a triangle with a certain property, then for every positive integer $r$ there exists $n_0(S)$ independent of $r$ such that every $r$-coloring of $\mathbb{E}^n$ with $n\ge n_0(S)$ contains a monochromatic or a rainbow congruent copy of $S$. Gehér, Sagdeev, and Tóth formalized this dimension independence as the canonical Ramsey property and proved it for all hypercubes, thereby covering rectangles whose squared aspect ratio $(a/b…

Commanders owners anticipate possible stadium name discussion Sunday with President Trump https://www.nytimes.com/athletic/6789811/2025/11/08/commanders-trump-stadium-name-communications/

Integrated Sensing, Communication, and Positioning in Cellular Vehicular Networks
Xin Tong, Zhaoyang Zhang, Yuzhi Yang, Yu Ge, Zhaohui Yang, Henk Wymeersch, M\'erouane Debbah
https://arxiv.org/abs/2510.02939

Integrated Sensing, Communication, and Positioning in Cellular Vehicular Networks
In this correspondence, a novel integrated sensing and communication (ISAC) framework is proposed to accomplish data communication, vehicle positioning, and environment sensing simultaneously in a cellular vehicular network. By incorporating the vehicle positioning problem with the existing computational-imaging-based ISAC models, we formulate a special integrated sensing, communication, and positioning problem in which the unknowns are highly coupled. To mitigate the rank deficiency and make i…

Medium Access for Multi-Cell ISAC through Scheduling of Radar and Communication Tasks
Jo\~ao Henrique Inacio de Souza, Fabio Saggese, Kun Chen-Hu, Petar Popovski
https://arxiv.org/abs/2510.05821

Medium Access for Multi-Cell ISAC through Scheduling of Radar and Communication Tasks
This paper focuses on communication, radar search, and tracking task scheduling in multi-cell integrated sensing and communication (ISAC) networks under quality of service (QoS) constraints. We propose a medium access control framework multiplexing the tasks while optimizing radar scan patterns through an interference-aware assignment formulation. Simulations show that our solution guarantees target QoS with improved resource efficiency over baseline schemes, highlighting the benefits of coordi…

Deformation quantisation of exact shifted symplectic structures, with an application to vanishing cycles
J. P. Pridham
https://arxiv.org/abs/2511.07602 https://arxiv.org/pdf/2511.07602 https://arxiv.org/html/2511.07602
arXiv:2511.07602v1 Announce Type: new
Abstract: We extend the author's and CPTVV's correspondence between shifted symplectic and Poisson structures to establish a correspondence between exact shifted symplectic structures and non-degenerate shifted Poisson structures with formal derivation, a concept generalising constructions by De Wilde and Lecomte. Our formulation is sufficiently general to encompass derived algebraic, analytic and $\mathcal{C}^{\infty}$ stacks, as well as Lagrangians and non-commutative generalisations. We also show that non-degenerate shifted Poisson structures with formal derivation carry unique self-dual deformation quantisations in any setting where the latter can be formulated.
One application is that for (not necessarily exact) $0$-shifted symplectic structures in analytic and $\mathcal{C}^{\infty}$ settings, it follows that the author's earlier parametrisations of quantisations are in fact independent of any choice of associator, and generalise Fedosov's parametrisation of quantisations for classical manifolds.
Our main application is to complex $(-1)$-shifted symplectic structures, showing that our unique quantisation of the canonical exact structure, a sheaf of twisted $BD_0$-algebras with derivation, gives rise to BBDJS's perverse sheaf of vanishing cycles, equipped with its monodromy operator.
toXiv_bot_toot

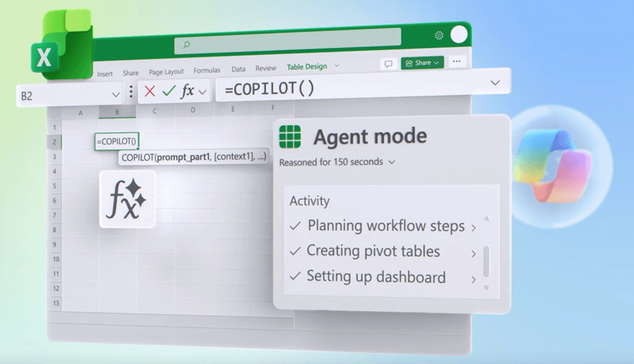
Been doing these demos for a month now & even the most jaded & cynical audience members all ask the same question:
"Um, so when is this coming out & how do I get it?" 😁
#Excel #Copilot #Microsoft

Shawn Brink (@Shawn_Brink@techhub.social)
Attached: 1 image Microsoft #Excel Power User Updates | Agent Mode, Copilot Function and Formula AI https://www.elevenforum.com/t/microsoft-excel-power-user-updates-agent-mode-copilot-function-and-formula-ai.41677/

Feit's conjecture, the canonical Brauer induction formula, and Adams operations
Robert Boltje, Gabriel Navarro
https://arxiv.org/abs/2510.03179 https://

Feit's conjecture, the canonical Brauer induction formula, and Adams operations
This paper is motivated by a strong version of Feit's conjecture, first formulated by the authors in joint work with A. Kleshchev and P. H. Tiep in 2025, concerning the conductor $c(χ)$ of an irreducible character $χ$ of a finite group $G$. We connect the conjecture with the following construction: For any positive integer $n$ dividing the exponent of $G$ and for any character $χ$ of $G$, we introduce an integer-valued invariant $S(G,χ,n)$ which can be defined as the sum of certain coeffici…

Culturally-Aware Conversations: A Framework & Benchmark for LLMs
Shreya Havaldar, Sunny Rai, Young-Min Cho, Lyle Ungar
https://arxiv.org/abs/2510.11563 https://

Culturally-Aware Conversations: A Framework & Benchmark for LLMs
Existing benchmarks that measure cultural adaptation in LLMs are misaligned with the actual challenges these models face when interacting with users from diverse cultural backgrounds. In this work, we introduce the first framework and benchmark designed to evaluate LLMs in realistic, multicultural conversational settings. Grounded in sociocultural theory, our framework formalizes how linguistic style - a key element of cultural communication - is shaped by situational, relational, and cultural …

Secrecy-Driven Beamforming for Multi-User Integrated Sensing and Communication
Ali Khandan Boroujeni, Hyeon Seok Rou, Ghazal Bagheri, Kuranage Roche Rayan Ranasinghe, Giuseppe Thadeu Freitas de Abreu, Stefan K\"opsell, Rafael F. Schaefer
https://arxiv.org/abs/2509.26249

Secrecy-Driven Beamforming for Multi-User Integrated Sensing and Communication
This paper proposes a secure integrated sensing and communications (ISAC) framework for multi-user systems with multiple communication users (CUs) and adversarial targets, where the design problem is formulated to maximize secrecy rate under joint sensing and communication constraints. An efficient solution is presented based on an accelerated fractional programming method using a non-homogeneous complex quadratic transform (QT), which decomposes the problem into tractable subproblems for beamf…

Pinching Antenna Systems (PASS) for Cell-Free Communications
Haochen Li
https://arxiv.org/abs/2510.03628 https://arxiv.org/pdf/2510.03628

Pinching Antenna Systems (PASS) for Cell-Free Communications
A pinching antenna system (PASS) assisted cell-free communication system is proposed. A sum rate maximization problem under the BS power budget constraint and PA deployment constraint is formulated. To tackle the proposed non-convex optimization problem, an alternating optimization (AO) algorithm is developed. In particular, the digital beamforming sub-problem is solved using the weighted minimum mean square error (WMMSE) method, whereas the pinching beamforming sub-problem is handled via a pen…