Tootfinder

Rep. Derrick Van Orden of Wisconsin’s Third District
wants you to think he is a tough guy.
He wears his Navy SEAL Trident like a shield, using his past service to deflect from the fact that he is a traitor to this country and tried to overthrow a democratically elected government on January 6th, 2021.
Derrick Van Orden is not a tough guy. He is a thug. And his race should be the number one target in Wisconsin.
Over the next year, we must strip away the costume and sh…

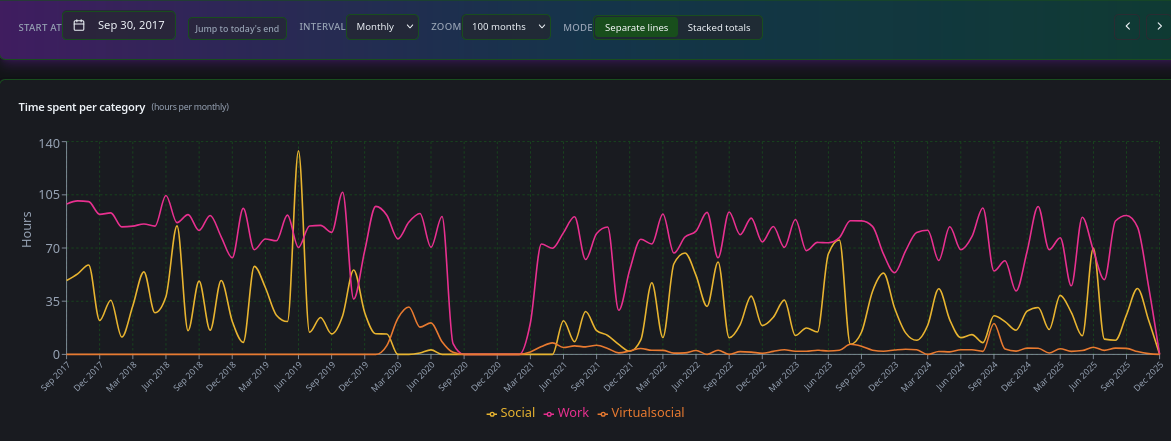
Added a zoom level to the Category page on the Exocortex-Log app. Can make the graphs look a lot cleaner now.
Looking back over the last 100 months here, we can see in general my social life is quite seasonal -- Festivals are a lot of social all weekend long and a couple of them in a month really bumps up the hours from my usual habit of sitting alone in a dark room pressing buttons.
The peak in 2019 is a summer filled with Glasto and Noisily and another festival or camping trip I don’t seem to have recorded the name of.
Then clearly visible is the drop-off in social activity as the COVID pandemic hit. Virtual-Social (IE zoom meetings and the like) picked up quite a bit around there but had died back to almost nothing way before the hours spent with actual people started to tick up.
Annoyingly, I have my biggest gap in data right on top of the pandemic there, where I failed to back up for months and then data became corrupted.
When the data-hole is over we see social life still not really returning until the middle of 2021 and not really getting back into stride until summer 2022.
It remains much lower now on average with lower peaks than before the pandemic too. Multiple reasons.
Work is pretty constant all the way though other than the data-hole. Dipping when I take time off for social mostly.
That data-hole is annoying. Back up your data kids.
#lifeLog #app #exocortexLog

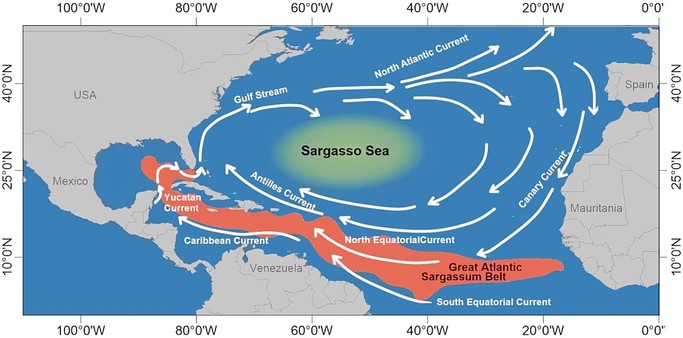
Weekend #Plankton Factoid 🦠🦐
Since 2011, millions of tons of a brown algae called Sargassum has washed onto beaches in the Caribbean. The rotting seaweed releases toxic hydrogen sulfide, smelling of rotten eggs, impacting tourism and shore access. It was initially thought Saharan iron dust was the cause, but new #science

Trump's latest pardons underscore the breadth of his efforts to clear anyone involved in efforts to overturn the 2020 election, which was won by Joe Biden.
Donald Trump on Friday issued a second pardon to Daniel Edwin Wilson,
whom he had previously pardoned for participation in the breach of the Capitol on Jan. 6, 2021,
but was in prison on a separate gun charge. The action was announced Saturday morning.

Trump also pardoned Suzanne Kaye, who had been sentenced to…

Trump gives second pardon to Jan. 6 participant and pardons two others
The latest pardons underscore the breadth of the efforts the president has taken to clear anyone involved in efforts to overturn the 2020 election results.

Heavy is the head that bows the crown. Or something…
https://apnews.com/article/bbc-director-resigns-trump-speech-editing-3aab83138d58c92db1bb00e77e568876

Top BBC bosses resign after criticism of the broadcaster’s editing of a Trump speech
The head of the BBC has resigned after criticism of the broadcaster’s editing of a speech by U.S. President Donald Trump. The BBC said that director-general Tim Davie and news CEO Deborah Turness both announced their resignations on Sunday. Britain’s public broadcaster has been criticized for editing a speech Trump made on Jan. 6, 2021 before protesters attacked the Capitol in Washington. Critics said that the way the speech was edited for a BBC documentary last year was misleading and cut …

What we know about the suspect in January 2021 D.C. pipe bomb case, DOJ says
https://www.nbcnews.com/news/us-news/brian-cole-jr-pipe-bomb-suspect-arrest-washington-dc-what-know-rcna247442

Ein Pariser Gericht hat #TotalEnergies wegen irreführender #Werbung zur #Klimaneutralität verurteilt.
Die Aussagen in einer Kampagne von 2021 stehen laut Urteil im Widerspruch …

Greenwashing-Prozess: Ölkonzern TotalEnergies wegen Greenwashing verurteilt
Weil er mit Klimaneutralität warb, ist der Ölkonzern TotalEnergies zu einer Geldstrafe wegen Greenwashing verurteilt worden. NGOs sehen ein "historisches Urteil".

The FBI has arrested a suspect five years after an unidentified person placed two pipe bombs outside the headquarters of the Republican and Democratic national parties in Washington.
Agents arrested Brian J. Cole Jr., 30, of Woodbridge, Virginia, on explosive charges.
Calls to relatives of Cole listed in public records were not immediately returned.
The mystery behind the person’s identity has bedeviled law enforcement and helped fuel conspiracy theories about Jan. 6, 2021, …

5 years later, authorities arrest a suspect in Washington pipe bomb case. Here's what to know
The FBI has arrested a suspect five years after an unidentified person placed two pipe bombs outside the headquarters of the Republican and Democratic national parties in Washington, D.C. The mystery behind the person’s identity has bedeviled law enforcement and helped fuel conspiracy theories about Jan. 6, 2021, and the Capitol riot by a mob of President Donald Trump’s supporters

from my link log —
The Nokia N900: the future that wasn’t.
https://www.osnews.com/story/133160/the-nokia-n900-the-future-that-wasnt/
saved 2021-03-18

Two West Virginia national guard members shot near the White House are in critical condition.
“What we know is that this is a targeted shooting,” Mayor Bowser said. “One individual appeared to have targeted these guardsmen.”
Law enforcement officials have identified a suspect, who is currently in custody,
as Rahmanullah Lakanwal,
an Afghan national who entered the United States in September 2021 and has been living in Washington state.